Quantum low-density parity-check (LDPC) codes are a leading approach to fault-tolerant quantum computation with low overhead, but practical decoding is challenging due to degeneracy and the abundance of short cycles in the underlying graphs. Our recent work develops modern decoding ideas (such as guided decimation, graph sparsification, and structure-exploiting erasure decoders) to make iterative decoding substantially more reliable while keeping complexity manageable.

A central theme is belief propagation (BP) enhanced with guided decimation, which incrementally fixes highly reliable qubits to encourage convergence and reduce decoding failures. We further adapt these ideas to the quantum erasure channel (motivated by “erasure conversion” in several hardware platforms), and we introduce new erasure-decoding strategies that apply broadly across quantum LDPC families. Complementary to this, we study the behavior of long hypergraph-product (HGP) code constructions and develop BP variants tailored to highly structured codes such as surface codes via principled graph sparsification.

• H. Yao, M. Gökduman, and H. D. Pfister, Cluster decomposition for improved erasure decoding of quantum LDPC codes, IEEE J. Sel. Areas Inf. Theory, vol. 6, pp. 176–188, 2025. arXiv PDF
• B. Zhang, H. Yao, and H. D. Pfister, Belief propagation decoding on a sparsified graph ensemble of the surface code, in Proc. IEEE Int. Symp. Inform. Theory (ISIT), 2025.
• M. Gökduman, H. Yao, and H. D. Pfister, The performance of long quantum LDPC codes based on the hypergraph product, in Proc. IEEE Int. Symp. Inform. Theory (ISIT), 2025.
• M. Gökduman, H. Yao, and H. D. Pfister, Erasure decoding for quantum LDPC codes via belief propagation with guided decimation, in Proc. Annual Allerton Conf. on Commun., Control, and Computing, pp. 1–8, 2024. arXiv PDF
• H. Yao, W. A. Laban, C. Häger, A. Graell i Amat, and H. D. Pfister, Belief propagation decoding of quantum LDPC codes with guided decimation, in Proc. IEEE Int. Symp. Inform. Theory (ISIT), pp. 2478–2483, 2024. arXiv PDF

Polar codes come with elegant low-complexity decoders (e.g., successive cancellation), but many important channels in practice are either unknown, have memory, or involve synchronization errors (insertions/deletions), where model-based decoding can be brittle or computationally expensive. Our recent work develops neural polar decoders (NPDs): data-driven decoders that preserve the polar decoding structure while replacing key update rules with small neural networks trained using only sample access to the channel. This enables decoding and code design even when an explicit channel model is unavailable, and it scales to channels with memory without trellis complexity that grows with the channel state size.

Beyond decoding, NPDs can provide accurate mutual information estimates and support data-driven rate/code optimization directly from channel observations. We further extend NPDs to synchronization-error settings, including deletion channels and realistic DNA data storage pipelines, achieving strong performance while reducing the complexity of classical trellis-based approaches. Finally, we study how NPDs integrate into end-to-end communication stacks (e.g., OFDM/single-carrier), including practical features such as rate matching and robustness across channel conditions.

• R. Hirsch, Z. Aharoni, H. D. Pfister, and H. H. Permuter, “A Study of Neural Polar Decoders for Communication,” arXiv preprint, arXiv:2510.03069, Oct. 2025. arXiv
• Z. Aharoni and H. D. Pfister, “Neural Polar Decoders for Deletion Channels,” in Proc. IEEE Int. Symp. Inform. Theory (ISIT), pp. 1–6, 2025. doi arXiv
• Z. Aharoni and H. D. Pfister, “Neural Polar Decoders for DNA Data Storage,” IEEE J. Sel. Areas Inf. Theory, vol. 6, pp. 403–416, 2025. doi arXiv
• Z. Aharoni, B. Huleihel, H. D. Pfister, and H. H. Permuter, “Code Rate Optimization via Neural Polar Decoders,” in Proc. IEEE Int. Symp. Inform. Theory (ISIT), pp. 2424–2429, IEEE, 2024. doi
• Z. Aharoni, B. Huleihel, H. D. Pfister, and H. H. Permuter, “Data-Driven Neural Polar Decoders for Unknown Channels With and Without Memory,” IEEE Trans. Inform. Theory, vol. 70, no. 12, pp. 8495–8510, 2024. doi
• Z. Aharoni, B. Huleihel, H. D. Pfister, and H. H. Permuter, “Data-Driven Polar Codes for Unknown Channels With and Without Memory,” in Proc. IEEE Int. Symp. Inform. Theory (ISIT), pp. 1890–1895, 2023. doi

Early “capacity via symmetry” results for Reed–Muller (RM) and other highly symmetric codes were first proved for erasure channels, where the analysis can leverage monotonicity and sharp threshold phenomena. More recent work shows that symmetry can also be leveraged far beyond erasures: for general binary memoryless symmetric (BMS) channels, the nested structure of RM codes provides multiple weakly correlated “looks” at each decoding stage, enabling recursive bounds on bit error under bit-MAP decoding at rates approaching capacity.

Building on this perspective, we develop proof techniques that (i) unify and simplify the BMS-channel analysis via symmetry + nesting, and (ii) strengthen the decay rates needed to move from bit reliability toward block reliability (notably using tools from the analysis of Boolean functions, including level-k / hypercontractive inequalities in the BSC case). We also extend “capacity via symmetry” ideas beyond binary alphabets—showing generalized RM codes achieve capacity on sufficiently symmetric non-binary channels—and into the classical-quantum setting, where new correlation bounds for quantum observables yield RM-style guarantees below the Holevo capacity for binary-input symmetric CQ channels.

• H. D. Pfister and G. Reeves, “Capacity on BMS Channels via Code Symmetry and Nesting,” arXiv preprint, arXiv:2504.15394, Apr. 2025. arXiv
• A. Mandal and H. D. Pfister, “Reed–Muller codes on CQ channels via a new correlation bound for quantum observables,” arXiv preprint, arXiv:2502.03785, Feb. 2025. arXiv
• G. Reeves and H. D. Pfister, “Achieving capacity on non-binary channels with generalized Reed–Muller codes,” in Proc. IEEE Int. Symp. Inform. Theory (ISIT), 2023. arXiv
• G. Reeves and H. D. Pfister, “Reed–Muller codes on BMS channels achieve vanishing bit-error probability for all rates below capacity,” IEEE Trans. Inform. Theory, 2023. arXiv online

Classical-quantum (CQ) channels model communication settings where the transmitter sends classical symbols but the receiver observes quantum states. This framework captures important regimes in optical communications and quantum sensing, where the ultimate performance limits are governed by quantum measurements and information measures such as the Holevo capacity. A central goal of our work is to understand when highly structured, practical coding and decoding methods can approach these quantum limits while remaining implementable with near-term quantum hardware.

We develop decoding and design tools for CQ channels that mirror the successes of classical coding theory. One thrust is belief propagation with quantum messages (BPQM): a message-passing approach that replaces classical beliefs by quantum systems and uses local quantum operations/measurements to perform inference and decoding. We extend BPQM beyond pure-state settings to binary-input symmetric CQ channels, and further to polar codes via a paired-measurement construction that admits a classical density-evolution analysis. In parallel, we study quantum receivers that exploit joint detection to unlock superadditive gains in optical links, and we investigate structural connections (e.g., dualities between classical channels and quantum pure-state channels). Finally, we explore CQ-flavored source/channel coding problems such as quantum state compression using polar-code structure, and we establish new analytical tools for algebraic codes (e.g., Reed–Muller codes) on CQ channels via correlation bounds for quantum observables.

• A. Mandal and H. D. Pfister, “Reed–Muller codes on CQ channels via a new correlation bound for quantum observables,” Proc. IEEE Int. Symp. Inform. Theory (ISIT), 2025 (accepted). arXiv
• J. Weinberg, A. Mandal, and H. D. Pfister, “Quantum state compression with polar codes,” Proc. IEEE Int. Symp. Inform. Theory (ISIT), pp. 2050–2055, 2024. arXiv DOI
• H. D. Pfister, C. Piveteau, J. M. Renes, and N. Rengaswamy, “Belief propagation for classical and quantum systems: Overview and recent results,” IEEE BITS the Information Theory Magazine , 2023. online
• A. Mandal, S. Brandsen, and H. D. Pfister, “Belief-propagation with quantum messages for polar codes on classical-quantum channels,” Proc. IEEE Int. Symp. Inform. Theory (ISIT), pp. 613–618, 2023. DOI arXiv
• S. Brandsen, A. Mandal, and H. D. Pfister, “Belief propagation with quantum messages for symmetric classical-quantum channels,” Proc. IEEE Information Theory Workshop (ITW), 2022. arXiv DOI
• N. Rengaswamy and H. D. Pfister, “On the duality between the BSC and quantum PSC,” Proc. IEEE Int. Symp. Inform. Theory (ISIT), pp. 2232–2237, 2021. DOI arXiv
• N. Rengaswamy, K. P. Seshadreesan, S. Guha, and H. D. Pfister, “A belief propagation-based quantum joint-detection receiver for superadditive optical communications,” Conf. Lasers and Electro-Optics (CLEO), May 2021. online
• N. Rengaswamy, K. P. Seshadreesan, S. Guha, and H. D. Pfister, “Belief propagation with quantum messages for quantum-enhanced classical communications,” npj Quantum Information, vol. 7, p. 97, 2021. journal arXiv
• N. Rengaswamy, K. P. Seshadreesan, S. Guha, and H. D. Pfister, “Quantum advantage via qubit belief propagation,” Proc. IEEE Int. Symp. Inform. Theory (ISIT), pp. 1824–1829, 2020. DOI

Modern communication systems have highly structured algorithms (equalization, decoding, detection, and inference) that already exploit domain knowledge. Our work asks a complementary question: which parts of these algorithms can be learned from data or simulation while preserving the underlying structure? A recurring theme is to embed learning into well-understood iterative architectures—so that the learned system remains interpretable, efficient, and compatible with existing communication pipelines.

On the classical coding side, we study learned iterative decoders that improve performance with modest additional complexity. This includes (i) learned belief-propagation decoding with simple parameter sharing and SNR adaptation, and (ii) reinforcement learning approaches that cast iterative decoding as a sequential decision problem (e.g., learned bit-flipping strategies), as well as methods to prune neural BP decoders to reduce complexity while maintaining near-ML performance for short codes. On the quantum side, we use learning and adaptive procedures to design measurement strategies for quantum multiple-hypothesis testing and discrimination of tensor-product quantum states—problems that are closely connected to detection and decoding over quantum channels.

• S. Brandsen, K. D. Stubbs, and H. D. Pfister, “Reinforcement learning with neural networks for quantum multiple hypothesis testing,” in Proc. IEEE Int. Symp. Inform. Theory (ISIT), pp. 1897–1902, 2020. arXiv DOI
• S. Brandsen, M. Lian, K. D. Stubbs, N. Rengaswamy, and H. D. Pfister, “Adaptive procedures for discriminating between arbitrary tensor-product quantum states,” in Proc. IEEE Int. Symp. Inform. Theory (ISIT), pp. 1933–1938, 2020. arXiv online
• A. Buchberger, C. Häger, H. D. Pfister, L. Schmalen, and A. Graell i Amat, “Pruning neural belief propagation decoders,” in Proc. IEEE Int. Symp. Inform. Theory (ISIT), 2020. arXiv DOI
• M. Lian, F. Carpi, C. Häger, and H. D. Pfister, “Reinforcement learning for channel coding,” in Proc. IEEE Intl. Zurich Seminar on Commun., p. 89, ETH Zurich, 2020. pdf
• F. Carpi, C. Häger, M. Martalò, R. Raheli, and H. D. Pfister, “Reinforcement learning for channel coding: Learned bit-flipping decoding,” in Proc. Annual Allerton Conf. on Commun., Control, and Comp., pp. 922–929, 2019. arXiv
• M. Lian, F. Carpi, C. Häger, and H. D. Pfister, “Learned belief-propagation decoding with simple scaling and SNR adaptation,” in Proc. IEEE Int. Symp. Inform. Theory (ISIT), pp. 161–165, 2019. arXiv
• M. Lian, C. Häger, and H. D. Pfister, “What can machine learning teach us about communications?,” in Proc. IEEE Information Theory Workshop (ITW), Guangzhou, China, 2018. arXiv DOI

Fiber-optic communication links carry virtually all intercontinental data traffic and are often referred to as the Internet backbone. The signal evolution in an optical fiber is implicitly described by the nonlinear Schrödinger equation, which is schematically illustrated in the above figure.

In this research, we explore the close connection between the propagation dynamics in optical fiber and deep learning. Our main observation is that the mathematical structure that results from applying spatial discretization methods (in particular the so-called split-step method) to the nonlinear Schrödinger equation is very similar to the structure of a conventional deep neural network with multiple layers. In a nutshell, the main idea is to obtain a machine-learning model by properly parameterizing the split-step method and viewing the linear steps as general linear functions, similar to the weight matrices in neural network. Compared to applying large neural networks (e.g., for signal equalization purposes), such physics-based machine-learning models are appealing because they incorporate important domain knowledge about the propagation dynamics directly into the model structure and obey well-established physical principles like symmetry and locality in order to reduce the number of trainable parameters. Moreover, these models also allow us to examine and interpret the learned solutions in order to understand why they perform well.

• C. Häger and H. D. Pfister, Physics-Based Deep Learning for Fiber-Optic Communication Systems, IEEE J. Sel. Areas Commun., vol. 39, no. 1, pp. 280-294, Jan. 2021
• V. Oliari, S. Goossens, C. Häger, G. Liga, R. M. Bütler, M. van den Hout, S. van der Heide, H. D. Pfister, C. Okonkwo, A. Alvarado, Revisiting Multi-Step Nonlinearity Compensation with Machine Learning: An Experimental Demonstration, J. Lightw. Technol., vol. 38, no. 12, pp. 3114-3124, June 2020
• C. Häger and H. D. Pfister, Wideband Time-Domain Digital Backpropagation via Subband Processing and Deep learning, in Proc. European Conf. Optical Communication (ECOC), Rome, Italy, 2018
• C. Fougstedt, C. Häger, L. Svensson, H. D. Pfister, P. Larsson-Edefors, ASIC Implementation of Time-Domain Digital Backpropagation with Deep-Learned Chromatic Dispersion Filters, in Proc. European Conf. Optical Communication (ECOC), Rome, Italy, 2018

Early work on algebraic codes often paid special attention to the symmetry of the code. With the rise of sparse random codes and iterative decoding, the idea that symmetry alone could lead to good performance started to seem rather implausible. However, in a breakthrough, we have shown that symmetry is actually sufficient to achieve capacity. Specifically, we proved that sequences of error-correcting codes with doubly-transitive permutation groups achieve capacity on erasure channels under symbol-wise maximum a posteriori (MAP) decoding. While the proof only holds for erasure channels, we believe the same result holds for general symmetric channels. This discovery was made independently by two groups: {Santhosh Kumar and myself} and {Shrinivas Kudekar, Marco Mondelli, Eren Sasoglu, and Ruediger Urbanke}.

This result solves the open problem of whether or not Reed-Muller codes achieve capacity for some rate bounded away from 0 and 1. This was a posted open problem from the 2015 Simons Institute program on Information Theory and the subject of a 1994 conjecture by Dumer and Farrell. It has also been discussed by many others including Arikan, Abbe, Shpilka, and Widgerson.

The same result also holds for primitive narrow-sense BCH codes and other classes of highly symmetric algebraic codes. Finally, the result for erasure channels has been extended to the quantum erasure channel and sequences of cyclic codes whose blocklengths have the proper numerology (e.g., increasing prime lengths suffice).

The conference paper was selected as Best Paper at STOC 2016 and the journal paper received the 2021 Information Theory Society Paper Award.

• S. Kudekar, S. Kumar, M. Mondelli, H. D. Pfister, E. Sasoglu, and R. Urbanke, “Reed-Muller codes achieve capacity on erasure channels,” accepted to IEEE Trans. Inform. Theory, 2016. arXiv
• S. Kudekar, S. Kumar, M. Mondelli, H. D. Pfister, E. Sasoglu, and R. Urbanke, “Reed-Muller codes achieve capacity on erasure channels,” in Proc. of the Annual ACM Symp. on Theory of Comp., 2016. paper slides
• S. Kudekar, S. Kumar, M. Mondelli, H. D. Pfister, and R. L. Urbanke, “Comparing the bit-MAP and block-MAP decoding thresholds of Reed-Muller codes on BMS channels,” in Proc. IEEE Int. Symp. Inform. Theory (Barcelona, Spain), pp. 1755–1759, 2016. arXiv
• S. Kumar, R. Calderbank, and H. D. Pfister, “Reed-Muller codes achieve capacity on the quantum erasure channel,” in Proc. IEEE Int. Symp. Inform. Theory (Barcelona, Spain), pp. 1750–1754, 2016.
• S. Kumar, R. Calderbank, and H. D. Pfister, “Beyond double transitivity: Capacity-achieving cyclic codes on erasure channels,” in Proc. IEEE Inform. Theory Workshop, pp. 241–245, Sept 2016.

From 2011-2012, Kudekar, Richardson, and Urbanke showed that low-density parity-check (LDPC) convolutional codes (or spatially-coupled codes) can approach capacity on the binary erasure channel (BEC) and binary-input memoryless symmetric channels. The mechanism behind this spectacular performance is the threshold saturation phenomenon, which is characterized by the belief-propagation noise threshold of the spatially-coupled ensemble increasing to an intrinsic noise threshold (e.g., the MAP threshold) defined by the uncoupled system. While these results are quite impressive, the proof technique in the above work leads to long and complicated proofs.

Our main result is a simple proof technique that establishes threshold saturation for a general class of spatially-coupled systems. It is based on potential functions and both simplifies and generalizes most previous results in this area.

• S. Kumar, A. J. Young, N. Macris, and H. D. Pfister, “Threshold saturation for spatially-coupled LDPC and LDGM codes on BMS channels,” submitted to IEEE Trans. on Inform. Theory, Nov. 2013. arXiv
• A. Yedla, Y.-Y. Jian, P. S. Nguyen, and H. D. Pfister, “A simple proof of Maxwell saturation for coupled scalar recursions,” submitted to IEEE Trans. on Inform. Theory, 2013. arXiv
• “Spatial coupling, potential functions, and the Maxwell construction,” slides. Annual Workshop on Information Theory and its Applications, San Diego, CA, Feb. 2013
• “From BP to MAP via Spatial Coupling,” slides. Wireless Networking and Communication Seminar, University of Texas, Austin, Nov. 9th, 2012
• “A Simple Proof of Threshold Saturation for Coupled Scalar Recursions,” slides. Stanford University, August 17th, 2012; Summer Research Institute, Ecole Polytechnique Federale de Lausanne, June 7th, 2012
• S. Kumar, A. J. Young, N. Macris, and H. D. Pfister, “A proof of threshold saturation for spatially-coupled LDPC codes on BMS channels,” in Proc. Annual Allerton Conf. on Commun., Control, and Comp., 2012.
• A. Yedla, Y. Y. Jian, P. S. Nguyen, and H. D. Pfister, “A simple proof of threshold saturation for coupled vector recursions,” in Proc. IEEE Inform. Theory Workshop, 2012. arXiv
• A. Yedla, Y.-Y. Jian, P. S. Nguyen, and H. D. Pfister, “A simple proof of threshold saturation for coupled scalar recursions,” in Proc. Int. Symp. on Turbo Codes & Iterative Inform. Proc., 2012. arXiv
• Y.-Y. Jian, H. D. Pfister, and K. R. Narayanan, “Approaching capacity at high rates with iterative hard-decision decoding,” in Proc. IEEE Int. Symp. Inform. Theory, pp. 2696–2700, 2012. arXiv

A noisy Slepian-Wolf problem is considered where two correlated sources are separately encoded and transmitted over two independent binary memoryless symmetric channels. Each channel capacity is assumed to be characterized by a single parameter which is not known at the transmitter. The receiver has knowledge of both the source correlation and the channel parameters. We call a system universal if it retains near-capacity performance without channel knowledge at the transmitter.

Kudekar et al. recently showed that terminated low-density parity-check (LDPC) convolutional codes (a.k.a. spatially-coupled LDPC ensembles) can have belief-propagation thresholds that approach their maximum a-posteriori thresholds. This was proven for binary erasure channels and shown empirically for binary memoryless symmetric channels. They also conjectured that the principle of spatial coupling is very general and the phenomenon of threshold saturation applies to a very broad class of graphical models.

In this research, we derive an area theorem for the joint decoder and empirically show that threshold saturation occurs for this problem. As a result, we demonstrate near-universal performance for this problem using the proposed spatially-coupled coding system. A similar result has also been obtained for the 2-user multiple-access channel.

• P. S. Nguyen, A. Yedla, H. D. Pfister, and K. R. Narayanan, “On the maximum a posteriori decoding thresholds of multiuser systems with erasures,” in Proc. IEEE Int. Symp. Inform. Theory (Cambridge, MA), pp. 2711–2715, July 2012.
• A. Yedla, P. S. Nguyen, H. D. Pfister, and K. R. Narayanan, “Universal codes for the Gaussian MAC via spatial coupling,” in Proc. Annual Allerton Conf. on Commun., Control, and Comp. (Monticello, IL), Sept. 2011. paper slides
• A. Yedla, H. Pfister, and K. Narayanan, “Universality for the noisy Slepian-Wolf problem via spatial coupling,” in Proc. IEEE Int. Symp. Inform. Theory (St. Petersburg, Russia), July 2011. paper slides

This research considers the relationship between code-rate selection and queueing performance for communication systems subject to time-varying channel conditions. While error-correcting codes offer protection against channel uncertainties, there exists a natural tradeoff between the enhanced protection of low-rate codes and the rate penalty imposed by additional redundancy. In the limiting regime where codewords are asymptotically long, this tradeoff is well-understood and characterized by the Shannon capacity. However, for delay-sensitive communication systems and finite block lengths, a complete characterization of this tradeoff is not fully developed. This research offers a new perspective on the queueing performance of communication systems with finite block lengths operating over correlated erasure channels. A rigorous framework that links code rate to overall system performance for random codes is presented and guidelines are identified for code-rate selection in delay-sensitive systems.

• S. Kumar, J.-F. Chamberland, and H. D. Pfister, “First-passage time and large-deviation analysis for erasure channels with memory,” in IEEE Trans. Inform. Theory, vol. 59, pp. 5547–5565, Sept. 2013.
• S. Kumar, J.-F. Chamberland, and H. D. Pfister, “Large deviations on empirical service for erasure channels with memory,” in Proc. Annual Allerton Conf. on Commun., Control, and Comp. (Monticello, IL), Sept. 2011. paper slides
• F. Hamidi-Sepehr, H. D. Pfister, and J. F. Chamberland, “On the queueing behavior of Gilbert-Elliott channels in the rare-transition regime,” in Proc. Conf. on Inform. Sciences and Systems, 2012. paper slides
• F. Hamidi-Sepehr, Y. Cai, H. D. Pfister, and J.-F. Chamberland, “Queueing behavior of the Gilbert-Elliott channel: BCH codes and Poisson arrivals,” in Proc. IEEE Int. Symp. Inform. Theory (St. Petersburg, Russia), July 2011. paper
• P. Parag, J.-F. Chamberland, H. D. Pfister, and K. R. Narayanan, “Code-rate selection, queueing behavior, and the correlated erasure channel,” in IEEE Trans. on Inform. Theory, vol. 59, pp. 397–407, Jan. 2013. arXiv
• P. Parag, J.-F. Chamberland, H. D. Pfister, and K. R. Narayanan, “On the queueing behavior of random codes over a Gilbert-Elliott erasure channel,” in Proc. IEEE Int. Symp. Inform. Theory (Austin, TX), pp. 1798–1802, June 2010. paper slides
• P. Parag, J.-F. Chamberland, H. D. Pfister, and K. R. Narayanan, “Code rate, queueing behavior and the correlated erasure channel,” in Proc. IEEE Inform. Theory Workshop (Cairo, Egypt), Jan. 2010. paper slides

Recently, it has been observed that terminated low-density-parity-check (LDPC) convolutional codes (or spatially-coupled codes) appear to approach the capacity universally across the class of binary memoryless channels. This is facilitated by the threshold saturation effect whereby the belief-propagation (BP) threshold of the spatially-coupled ensemble is boosted to the maximum a-posteriori (MAP) threshold of the underlying constituent ensemble.

We consider the universality of spatially-coupled codes over intersymbol-interference (ISI) channels under joint iterative decoding. More specifically, we empirically show that threshold saturation also occurs in this case. This can be observed by identifying the EXIT/GEXIT curves that naturally obey the general area theorem. From these curves, the corresponding MAP and the BP thresholds are then numerically obtained and threshold saturation is observed.

• P. S. Nguyen, A. Yedla, H. D. Pfister, and K. R. Narayanan, “Spatially-coupled codes and threshold saturation on intersymbol-interference channels,” to be submitted to IEEE Trans. on Inform. Theory, 2012. arXiv
• P. S. Nguyen, A. Yedla, H. D. Pfister, and K. R. Narayanan, “Threshold saturation of spatially-coupled codes on intersymbol-interference channels,” IEEE Int. Conf. Commun., Jan. 2012. paper slides
• C. Wang and H. D. Pfister, “Upper bounds on the MAP threshold of iterative decoding systems with erasure noise,” in Proc. Int. Symp. on Turbo Codes & Related Topics, Lausanne, Switzerland, Sep. 2008. paper slides (this pdf has been updated to correct a typo in Lemma 3)

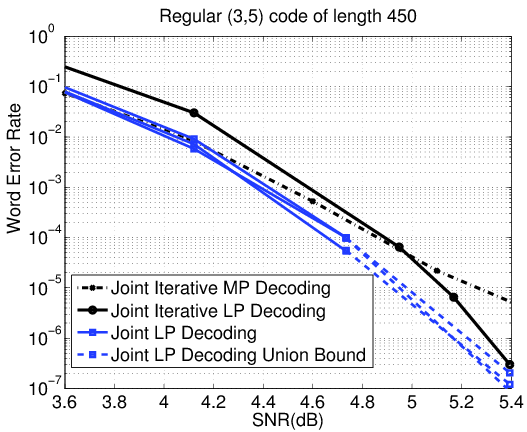
This research considers the joint-decoding problem for finite-state channels (FSCs) and low-density parity-check (LDPC) codes. First, the linear-programming (LP) decoder for binary linear codes is extended to joint-decoding of binary-input FSCs. In particular, we provide a rigorous definition of LP joint-decoding pseudo-codewords that enables evaluation of the pairwise error probability between codewords and pseudocodewords in AWGN. This leads naturally to a provable upper bound on decoder failure probability. If the channel is a finite-state intersymbol interference channel, then the joint LP decoder also has the maximum-likelihood (ML) certificate property and all integer-valued solutions are codewords. After deriving these results, we discovered some elements were equivalent to earlier work by Flanagan on linear-programming receivers. In the second part, we develop an efficient iterative solver for the joint LP decoder discussed in the first part.

Next, we extend the approach of iterative approximate LP decoding, proposed by Vontobel and Koetter and analyzed by Burshtein, to this problem. By taking advantage of the dual-domain structure of the joint-decoding LP, we obtain a convergent iterative algorithm for joint LP decoding whose structure is similar to BCJR-based turbo equalization (TE). The result is a joint iterative decoder whose per-iteration complexity is similar to that of TE but whose performance is similar to that of joint LP decoding. The main advantage of this decoder is that it appears to provide the predictability of joint LP decoding and superior performance with the computational complexity of TE. One expected application is coding for magnetic storage where the required block-error rate is extremely low and system performance is difficult to verify by simulation.

• Byung-Hak Kim and H. D. Pfister, “Joint decoding of LDPC codes and finite-state channels via linear programming,” in IEEE J. Select. Topics in Signal Proc., vol. 5, pp. 1563–1576, Dec. 2011.
• B.-H. Kim and H. D. Pfister, “An iterative joint linear-programming decoding of LDPC codes and finite-state channels,” in Proc. IEEE Int. Conf. Commun., June 2011. arXiv
• B.-H. Kim and H. D. Pfister, “On the joint decoding of LDPC codes and finite-state channels via linear programming,” in Proc. IEEE Int. Symp. Inform. Theory (Austin, TX), pp. 754–758, June 2010. paper slides

One popular approach to soft-decision decoding of Reed-Solomon (RS) codes is based on using multiple trials of a simple RS decoding algorithm in combination with erasing or flipping a set of symbols or bits in each trial. We consider a novel framework based on rate-distortion (RD) theory to analyze these multiple-decoding algorithms. By defining an appropriate distortion measure between an error pattern and an erasure pattern, the successful decoding condition, for a single errors-and-erasures decoding trial, becomes equivalent to distortion being less than a fixed threshold.

Finding the best set of erasure patterns also turns into a covering problem that can be solved asymptotically by RD theory. Thus, the proposed approach can be used to understand the asymptotic performance-versus-complexity tradeoff of multiple errors-and-erasures decoding of RS codes. This initial result is also extended a few directions. The rate-distortion exponent (RDE) is computed to give more precise results for moderate blocklengths. Multiple trials of algebraic soft-decision (ASD) decoding are analyzed using this framework. Analytical and numerical computations of the RD and RDE functions are also presented. Finally, simulation results show that sets of erasure patterns designed using the proposed methods outperform other algorithms with the same number of decoding trials.

• P. S. Nguyen, H. D. Pfister, and K. R. Narayanan, “On multiple decoding attempts for Reed-Solomon codes: A rate-distortion approach,” in IEEE Trans. on Inform. Theory, vol. 57, pp. 668–691, Feb. 2011. arXiv
• P. S. Nguyen, H. D. Pfister, and K. R. Narayanan, “A rate-distortion exponent approach to multiple decoding attempts for Reed-Solomon codes,” in Proc. IEEE Int. Symp. Inform. Theory (Austin, TX), pp. 1798–1802, June 2010. paper slides
• P. S. Nguyen, H. D. Pfister, and K. R. Narayanan, “A rate-distortion perspective on multiple decoding attempts for Reed-Solomon codes,” in Proc. 47th Annual Allerton Conf. on Commun., Control, and Comp. (Monticello, IL), pp. 1235–1242, Oct. 2009. paper slides

This work began with the observation that compressed sensing can be seen as a real-number extension of syndrome source-coding. Since coding over the real numbers is akin to using a very large alphabet, we applied coding techniques designed for large alphabets to compressed sensing. In particular, we used low-density measurement matrices with verification decoding and were able to derive rigorous sparsity thresholds based on density evolution.

• “The effect of spatial coupling on compressive sensing,” in Proc. Annual Allerton Conf. on Commun., Control, and Comp. (Monticello, IL), 2010. arXiv
• “Information Theory and Coding for Compressed Sensing,” slides. Center for Wireless Communications Ericsson Seminar, University of California, San Diego, March 2, 2009.
• F. Zhang and H. D. Pfister, “Verification decoding of high-rate LDPC codes with applications in compressed sensing,” in IEEE Trans. on Inform. Theory, vol. 58, pp. 5042–5058, Aug. 2012. arXiv
• F. Zhang and H. D. Pfister, “Analysis of verification-based decoding on the q-ary symmetric channel for large q,” in IEEE Trans. on Inform. Theory, vol. 57, pp. 6754–6770, Oct. 2011. arXiv
• F. Zhang and H. D. Pfister, “On the iterative decoding of high rate LDPC codes with applications in compressed sensing,” in Proc. 46th Annual Allerton Conf. on Commun., Control, and Comp. (Monticello, IL), Sep. 2008. paper slides
• F. Zhang and H. D. Pfister, “Compressed Sensing and Linear Codes over Real Numbers,” in Proc. 2008 Workshop on Inform. Theory and Appl., UCSD, La Jolla, CA, Feb. 2008. paper slides

This work provided the first capacity-achieving code ensembles for the binary erasure channel whose iterative decoding complexity (per information bit) is bounded as the gap to capacity vanishes. First, we designed irregular repeat accumulate (IRA) codes where all systematic bits were punctured. Later, we found a systematic construction based on accumulate repeat accumulate (ARA) codes.

• “Capacity-Achieving Codes for the BEC with Bounded Complexity,” slides. Texas A&M University, April 2006.
• H. D. Pfister and I. Sason, “Accumulate-repeat-accumulate codes: Capacity-achieving ensembles of systematic codes for the erasure channel with bounded complexity,” in IEEE Trans. on Inform. Theory, vol. 53(6), pp. 2088–2115, June 2007. paper
• H. D. Pfister and I. Sason, “Capacity-achieving ensembles of accumulate-repeat-accumulate codes for the erasure channel with bounded complexity,” in Proc. 2006 Workshop on Inform. Theory and Appl., UCSD, La Jolla, CA, Feb. 2006. paper slides
• H. D. Pfister, I. Sason, and R. Urbanke, “Capacity-achieving ensembles for the binary erasure channel with bounded complexity,” in IEEE Trans. on Inform. Theory, vol. 51(7), pp. 2352–2379, July 2005. paper
• H. Pfister, I. Sason, and R. Urbanke, “Bounds on the decoding complexity of punctured codes on graphs,” in Proc. 42nd Allerton Conf. on Comm., Control and Computing, Monticello, Illinois, pp. 481–491, Sept. 2004. paper

This work is based on a simple Monte Carlo algorithm that estimates information rates of finite-state intersymbol-interference channels. Before this, the best approach was very complex and yielded only loose bounds. This algorithm (which was also discovered independently by Arnold and Loeliger) stimulated enough interest in this area that, a few years later, these capacities can now be computed to almost any desired accuracy. This work was later extended to provably design irregular LDPC codes that achieve the i.i.d. capacity of some erasure channels with memory.

• H. D. Pfister, “The capacity of finite-state channels in the high-noise regime,” in Entropy of Hidden Markov Processes and Connections to Dynamical Systems (B. Marcus, K. Petersen, and T. Weissman, eds.), Cambridge University Press, 2011. arXiv
• H. D. Pfister and P. H. Siegel, “Joint iterative decoding of LDPC codes for channels with memory and erasure noise,” in IEEE J. Select. Areas Commun., vol. 26(2), pp. 320–327, Feb. 2008. paper
• J. B. Soriaga, H. D. Pfister, and P. H. Siegel, “Determining and approaching achievable rates of binary intersymbol interference channels using multistage decoding,” in IEEE Trans. on Inform. Theory, vol. 53(4), pp. 1416–1429, April 2007. (IEEE COMSOC Data Storage Best Paper 2008) paper
• J. B. Soriaga, H. D. Pfister, and P. H. Siegel, “On the low-rate Shannon limit for binary intersymbol interference channels,” in IEEE Trans. on Communications, vol. 51(12), pp. 1962–1964, Dec. 2003. paper
• “On the Capacity of Finite-State Channels,” slides. Technion Institute, Haifa, Israel, March 2005.
• H. D. Pfister and P. H. Siegel, “Joint iterative decoding of LDPC codes and channels with memory,” in Proc. 3rd Intl. Symp. on Turbo Codes and Related Topics, Brest, France, pp. 15–18, Sep. 2003. paper slides
• H. D. Pfister, “The Capacity of Finite State Channels,” PhD Thesis Chapter 4, 2003. pdf
• H. D. Pfister, “Joint Iterative Decoding of LDPC Codes and Channels with Memory,” PhD Thesis Chapter 5, 2003. pdf
• H. D. Pfister, J. B. Soriaga, and P. H. Siegel, “On the achievable information rates of finite state ISI channels,” in Proc. IEEE Globecom, San Antonio, TX, pp. 2992–2996, Nov. 2001. paper slides